نوسانات مرسوم‌ترین معیار اندازه‌گیری ریسک هستند، اما آن‌ها به چند صورت بررسی می‌گردند. در مقاله قبلی، ما نشان دادیم که چگونه نوسانات تاریخی ساده را محاسبه می‌کنیم. در این مقاله، ما وارد بحث پیشرفته‌تر نوسانات ساده و بررسی میانگین متحرک‌های وزنی نمایی می‌شویم.

نوسانات تاریخی در مقابل نوسانات ضمنی

اول، اجازه دهید چشم‌اندازی از این معیار ارائه دهیم. دو روش گسترده وجود دارد: نوسانات تاریخی و ضمنی . در رویکرد تاریخی فرض می‌گردد که گذشته پیش‌درآمدی از آینده است؛ ما تاریخ را به این امید بررسی می‌کنیم که برای پیش‌بینی به ما کمک کند. در طرف دیگر، نوسانات ضمنی تاریخ را نادیده می‌گیرد؛ این روش نوسانات را با توجه به قیمت‌های بازار بررسی می‌کند. انگیزه استفاده از این روش این است که بازار بهتر از هر کسی می‌داند و قیمت‌های بازار ،هرچند ضمنی، یک هوشیاری نسبت به نوسانات دارد.

گر تمرکز ما تنها بر روی سه دیدگاه اساسی تاریخی باشد( بالا سمت چپ) آن‌ها دارای دو مرحله مشترک هستند:

• محاسبه سری بازده دوره
• اعمال یک طرح وزن‌دهی

اول،ما بازدهی دوره را محاسبه می‌کنیم. که یک سری داده از بازده‌های روزانه است که خود شامل بازده‌های مرکب نیز می‌باشد. برای هر روز، ما لگاریتم طبیعی قیمت سهم را می‌گیریم(به عنوان مثال قیمت امروز سهم را تقسیم بر قیمت دیروز می‌کنیم).

که در آن :

بازده روزi U_i =

قیمت سهم در روز i = S_i

قیمت سهم در روز قبل از روز i =   S_i-1

این کار منجر به تولید یک سری داده‌ها از بازده روزانه می‌گردد،یعنی از U_i تا U_i-m، بسته به اینکه ما چند روز در نظر بگیریم(m=روزها).

این کار ما را به مرحله دوم می‌برد. این جایی است که سه رویکرد با هم تفاوت پیدا می‌کنند. در مقاله قبلی، ما با استفاده از چند ساده‌سازی نشان دادیم که، واریانس ساده همان میانگین مجذور بازده‌ها است.

که در آن:

تعداد روزها= m

روزi =  n

اختلاف بازده و میانگین بازده= u

توجه داشته باشید که که این مجموع بازده‌های دوره‌ای، بعدا تقسیم بر تعداد روزها یا مشاهدات(m) می‌گردد. بنابراین، واقعا چیزی جز میانگین مجذور بازده‌ دوره نیست. به عبارت دیگر، به هر مجذور بازده وزن مساوی داده شده است. بنابراین اگر آلفا (a) یک عامل وزن‌دهی است(به طور خاص، a = 1/m )، پس واریانس ساده چیزی شبیه به این می‌گردد:

بهبود واریانس ساده با استفاده از EWMA

ضعف این روش این است که تمام بازدهی کسب شده وزن یکسانی می‌گیرد. بازده دیروز(جدیدترین بازده) تاثیر بیشتری نسبت به بازده یک ماه قبل بر روی واریانس ندارد. این مشکل با استفاده از میانگین متحرک وزنی نمایی (EWMA)، که در آن بازده اخیر دارای وزن بیشتری بر واریانس است، حل می‌گردد.

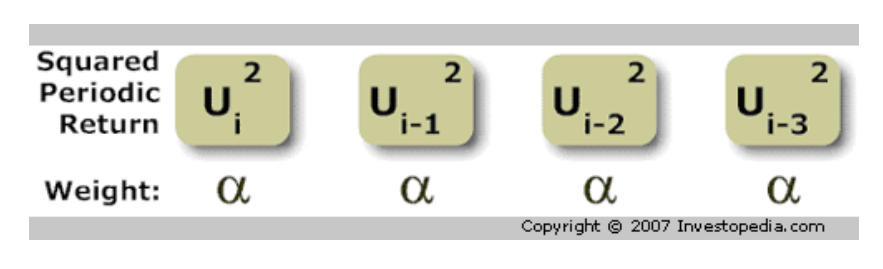
میانگین متحرک موزون نمایی (EWMA) لامدا(Lambda) (لاندا:مرسوم در فارسی) را معرفی می‌کند که یک متغیر ملایم‌کننده است. لامدا باید کمتر از یک باشد. تحت آن شرایط، به جای وزن مساوی، هر مجذور بازده به شکل زیر یک ضریب می‌گیرد.

به عنوان مثال، ریسک متریکس  ، یک شرکت مدیریت ریسک مالی، تمایل به استفاده از یک لامدا معادل 0.94 یا 94٪ دارد. در این مورد، وزن اولین (جدیدترین) مربع بازده دوره برابر است با  (0.94-1)⁰(0.94)=6% مربع بازده بعدی وزنی بر اساس ضریب لامدای قبلی می‌گیرد؛در این مورد 6٪ ضرب در 94٪ = 5.64٪ و وزن روز سوم برابر است با ²(0.94)(0.94-1)=5.30%.

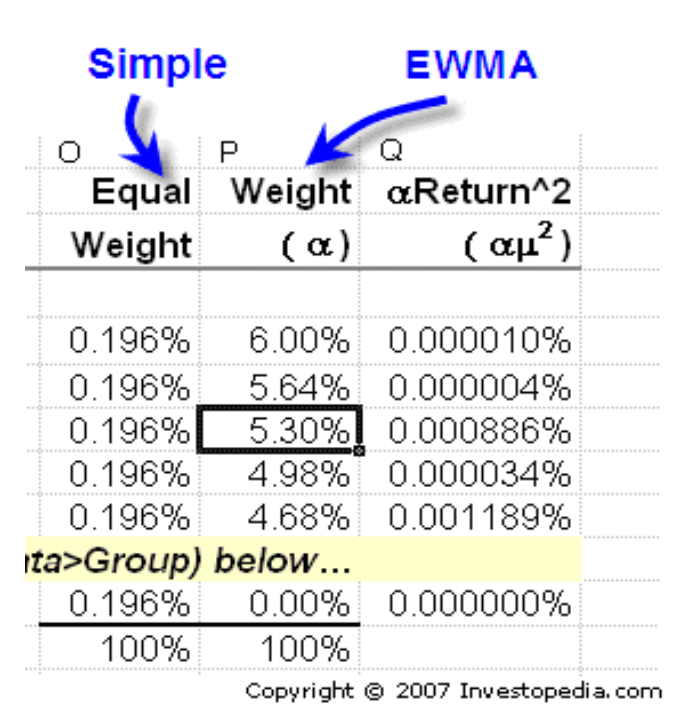
این معنای واژه "نمایی" در EWMA است: هر وزن ضریب ثابتی از وزن روز قبل است(یعنی لامدا که باید مقدارش زیر 1 باشد). این تضمین می کند که واریانس به شکلی وزن می‌گیرد که داده‌های جدید اهمیت بیشتری داشته باشند. تفاوت بین نوسانات ساده و EWMA برای GOOGLE در زیر به نمایش درآمده است.

همانطور که در ستون O می‌بینید نوسانات ساده وزن برابری معادل 0.196٪ به بازده هر دوره داده‌اند(داده‌های ما برای دو سال از قیمت سهم موجود است. که باعث می‌گردد ما 509 بازدهی روزانه داشته باشیم و 1/509=0.196٪). اما توجه کنید که در ستون P وزن 6٪، و سپس 5.64٪، و سپس 5.3٪ و به همین منوال ، به داده‌ها اختصاص داده شده است. این تنها تفاوت بین واریانس ساده و EWMA است.

به یاد داشته باشید: بعد از اینکه ما کل سری‌ها را با هم جمع زدیم (در ستونQ) به یک واریانس می‌رسیم که که همان مجذور انحراف معیار است. اگر ما نوسانات را می‌خواهیم باید به یاد داشته باشیم که ریشه دوم واریانس را بدست بیاوریم.

چه تفاوتی در نوسانات روزانه بین واریانس و EWMA در مورد گوگل وجود دارد؟ قابل توجه است که: واریانس ساده به ما نوسانات روزانه معادل 2.4٪ را داد اما EWMA نوسانات روزانه معادل 1.4 درصد را به ما داد. پس به ظاهر نوسانات گوگل اواخر کمتر شده است و به همین دلیل است که مقدار واریانس ساده بیش از EWMA است.

واریانس امروز یک تابع از واریانس روز قبل است

شما متوجه خواهید شد که ما نیاز به محاسبه یک سری طولانی از وزن‌های نمایی با روند کاهشی خواهیم داشت. ما اینجا به انجام عملیات ریاضی نمی‌پردازیم، اما یکی از بهترین ویژگی‌های EWMA این است که کل سری به راحتی با یک فرمول بازگشتی کاهش می‌یابد:

که در آن:

درجه کاهش وزن=  λ

مقدار واریانس دوره n =

مقدار میانگین متحرک وزنی نمایی(EWMA) دوره n = u²

بازگشتی به این معنی است که واریانس امروز به واریانس روز قبل وابسته است.  شما با استفاده از روش محاسبات طولانی نیز دقیقا به همین نتیجه خواهید رسید. این روش می گوید: واریانس امروز (تحت EWMA) برابر واریانس دیروز (وزن‌دهی شده توسط لامدا) به علاوه مربع بازده دیروز (وزن‌دهی شده با یک منهای لاندا)است. توجه کنید که چگونه ما دو بخش را با هم جمع کردیم: واریانس وزن‌دهی شده دیروز و  مجذور بازده وزن‌دهی شده دیروز.

با این حال، لامدا پارامتر تعدیل‌ کننده ما است. لامدای بالاتر( مانند لامدای RiskMetric که 94٪ است) نشان‌دهنده تجزیه کندتر سری داده ها است-در شرایط نسبی ما در حال حرکت به سمت داده‌های بیشتر در سری هستیم و  وزن آن‌ها آهسته‌تر کاهش می‌یابد. از سوی دیگر، اگر ما لامدا را کاهش دهیم، به سمت تجزیه سریع‌تر حرکت می‌کنیم: یعنی وزن داده‌ها سریعتر کاهش می‌یابد و در نتیجه تجزیه و از بین رفتن داده‌ها سریع‌تر خواهد بود و تعداد داده‌ها کمتر خواهد شد. (در این جدول محاسباتی، لامدا یک ورودی است، بنابراین شما می توانید حساسیت آن را بسنجید).

خلاصه

نوسانات همان انحراف از معیار سریع سهم و رایج‌ترین روش سنجش ریسک است. همچنین نوسانات ریشه دوم واریانس نیز هست. ما می توانیم واریانس را به صورت تاریخی یا به طور ضمنی (نوسانات ضمنی) اندازه گیری کنیم. هنگام اندازه گیری تاریخی، ساده ترین روش واریانس ساده است. اما ضعف واریانس ساده این است که تمام بازده‌ها وزن برابر می‌گیرند. بنابراین ما با یک معامله کلاسیک روبرو هستیم: ما همیشه داده های بیشتر می‌خواهیم اما داده‌های ما هر چه بیشتر باشد محاسبات ما با زمان حال فاصله بیشتری دارد (کم معنی‌تر است) . میانگین متحرک وزن‌دهی شده نمایی (EWMA) واریانس ساده را با استفاده از وزدن‌دهی به بازده هر دوره بهبود می‌بخشد. با انجام این کار، ما می توانیم از حجم نمونه بیشتری استفاده کنیم و در عوض وزن بیشتری به بازده‌های دوره‌های جدیدتر بدهیم.