منحنی ناقوسی چیست؟

منحنی ناقوسی(منحنی بل) یک نوع رایج از توزیع برای یک متغیر است ، همچنین به عنوان توزیع نرمال شناخته می‌گردد. اصطلاح "منحنی بل" سرچشمه از این واقعیت دارد که نموداری که برای ترسیم یک توزیع نرمال مورد استفاده قرار میگیرد شکلی مانند یک زنگوله یا ناقوس متقارن دارد.

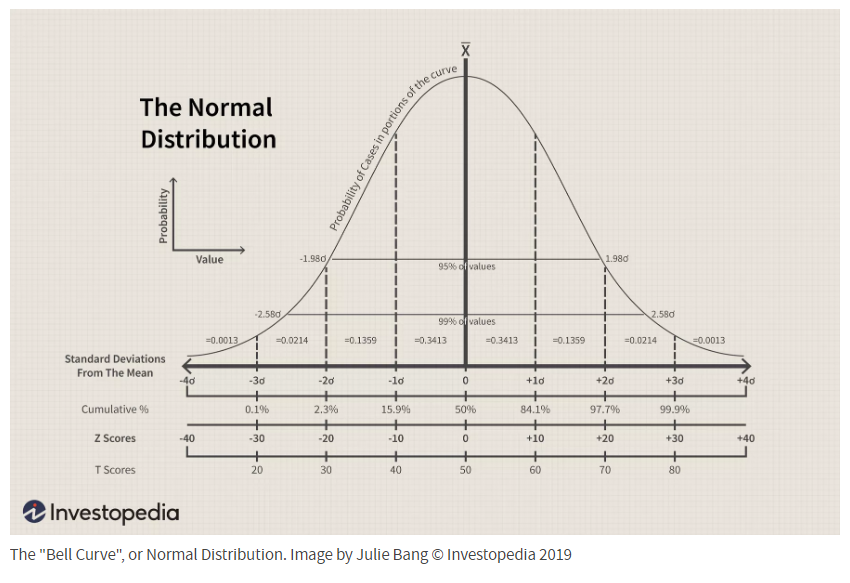
بلندترین نقطه روی منحنی، و یا بالای زنگ، نشان دهنده رویدادی با بیشترین احتمال رخ دادن در سری زمانی است( در اینجا به معنای میانگین، مد و میانه نیز هست)، این در حالی است که دیگر احتمالات به صورت قرینه اطراف این نقطه واقع گردیده اند و در هر دو طرف پیک یک قوس نزولی داریم. عرض منحنی بل توسط انحراف استاندارد آن تعریف می‌گردد.

نکات کلیدی

• منحنی زنگوله‌ای یک توزیع نرمال را نمایش می‌دهد که شکلی شبیه به زنگوله دارد.
• قله منحنی نشان دهنده میانگین، مد و میانه داده های جمع آوری شده است.
• انحراف استاندارد آن عرض نسبی منحنی زنگوله‌ای را در اطراف میانگین به تصویر می‌کشد.
• منحنی بل (توزیع نرمال) به طور معمول در آمار، از جمله در تجزیه و تحلیل داده های اقتصادی و مالی استفاده می شود.

منحنی ناقوسی چه اطلاعاتی به ما می‌دهد؟

اصطلاح "منحنی بل" برای توصیف یک تصویر از توزیع نرمال احتمال است که اساس شکل زنگوله‌ای آن انحراف استاندارد از میانگین است.  انحراف استاندارد یک روش سنجش عددی تنوع پراکندگی داده‌ها در مجموعه‌ای از مقادیر اطراف میانگین است. میانگین، به نوبه خود، اشاره به متوسط تمام نقاط داده در مجموعه داده ها یا سری داده ها دارد و بالاترین نقطه منحنی زنگوله‌ای را به ما می‌دهد.

تحلیل‌گران مالی و سرمایه گذاران اغلب از یک توزیع نرمال هنگام تجزیه و تحلیل بازده اوراق بهادار یا حساسیت بازار استفاده می‌کنند. در امور مالی، انحراف استاندارد بازده اوراق بهادار را نشان می‌دهد که به عنوان نوسانات شناخته می‌گردد.

 به عنوان مثال، سهامی که بر اساس منحنی زنگوله‌ای عمل می‌کند معمولا به عنوان سهام مرغوب شناخته می‌شود و نوسانات کمتری دارد و رفتار و الگوهای قابل پیش‌بینی‌تری دارد. سرمایه گذاران از توزیع نرمال بازده گذشته یک سهم به فرضیاتی از بازده‌ آتی سهم دست پیدا می‌کنند.

علاوه بر این معلمان نیز از منحنی زنگوله‌ای برای مقایسه نتایج امتحانات استفاده می‌کنند، به طور کلی منحنی زنگوله‌ای در دنیای آمار کاربرد بسیار گسترده‌ای دارد. منحنی زنگوله‌ای همچنین گاهی اوقات در مدیریت عملکرد و بکارگیری کارکنان در حد میانگین منحنی زنگوله‌ای کاربرد دارد. افراد با عملکرد بسیار بالا و همچنین افرادی با پایین‌ترین عملکرد در دو طرف پایین منحنی نزولی قرار می‌گیرند. این امر برای شرکت‌های بزرگ در زمان بررسی عملکرد و یا در زمان اتخاذ تصمیمات مدیریتی بسیار مفید است.

 مثالی از نحوه استفاده از منحنی زنگوله‌ای

عرض منحنی ناقوسی(زنگوله‌ای)  انحراف استاندارد آن است که به عنوان سطح تنوع داده های نمونه در اطراف میانگین محاسبه می‌گردد. به عنوان مثال، در منحنی زنگوله‌ای اگر تعداد 100 نمره از یک آزمون جمع‌آوری گردد ، برای اینکه توزیع نمرات نرمال باشد، 68٪ از نمرات باید در یک انحراف استاندارد بالاتر یا پایین‌تر از میانگین قرار بگیرند. حرکت دو انحراف استاندارد و دور شدن آن از میانگین باعث می‌گردد که 95٪ نمرات را شامل شود. حرکت سه انحراف استاندارد از میانگین باید 99.7 درصد از نمرات را شامل شود(شکل بالا را ببینید).

آن نمرات آزمون،مانند0 یا 100، که شدیدا پرت هستند به عنوان داده‌هایی در نظر گرفته می‌شوند که بیرون از محدوده سه انحراف استاندارد قرار می‌گیرند.

تفاوت بین منحنی زنگوله‌ای و منحنی غیر نرمال توزیع

با این حال،فرض توزیع نرمال همیشه در دنیای تجارت برقرار نیست. ممکن است سهام یا دیگر اوراق بهادار گاهی اوقات توزیع غیر نرمال داشته باشند که موجب از بین رفتن حالت زنگوله‌ای منحنی می‌گردد.

 توزیع غیر نرمال دارای انتهای پن‌تر از یک منحنی توزیع نرمال است.. انتهای پهن‌تر سیگنال‌های منفی به سرمایه‌گذاران می‌دهد و احتمال بیشتری برای بازده منفی قائل می‌شود.

محدودیت های استفاده از منحنی ناقوسی

 درجه بندی و یا ارزیابی عملکرد با استفاده از یک منحنی نرمال موجب دسته‌بندی مردم در رده‌های ضعیف،متوسط یا خوب می‌گردد. برای گروه های کوچک تر، نیاز به دسته‌بندی تعدادی از افراد در هر دسته برای شکل‌دهی منحنی نرمال موجب زیان بعضی افراد می‌گردد. به همان شکل گاهی اوقات، ممکن است همه افراد دانش‌آموزان و یا کارگران متوسط یا خوبی باشند ولی احتیاج به دسته‌بندی برای شکل‌دهی به منحنی نرمال موجب می‌گردد بعضی افراد به اجبار در دسته ضعیف قرار بگیرند. در واقعیت، داده‌ها کاملا نرمال نیستند. گاهی اوقات چولگی - و یا عدم تقارن بین صعود به سمت میانگین و نزول از میانگین - وجود دارد. در مواقع دیگر انتهای پهن (کشیدگی بیش از حد)، موجب می‌گردد که احتمال اتفاق افتادن وقایع انتهای منحنی بیش از چیزی باشد که توزیع نرمال پیشبینی کرده.